[论文] Data-Efficient Hierarchical Reinforcement Learning(HIRO)

---

一、概述

1. 提出一种较为通用的，去除繁杂假设的，高效的算法层次强化学习算法框架；

2. 框架

   $High-Level \space\space\space\space\space {———>}^{auto} \space\space\space\space Goal ————> ^{supervised} \space\space\space\space Low-Level controller$

3. 使用Off-Policy进行High-level及Low-level训练，通用化的设计，使得较好的在low-level controller中使用DDPG，TD3等确定性、off-policy的算法，兼容性强；

4. 提出针对于High-level的Off-Policy Correction。

---

二、 方法

HIRO(HIerarchical Reinforcement learning with Off-policy correction)

• [Low-level $\mu^{lo}$]
  1. 使用 Parameterized reward function 来表达特定的底层策略(潜在的无穷集合)；
  2. 通过训练相关策略，使其能够将obs $S_t$ 与期望Goal $g_t$相匹配。
• [High-level $\mu^{hi}$]
  1. 为temporally-extended experience选择目标序列；
  2. 使用off-policy correction使得其可以使用过往经验，来适应新的底层控制器策略。

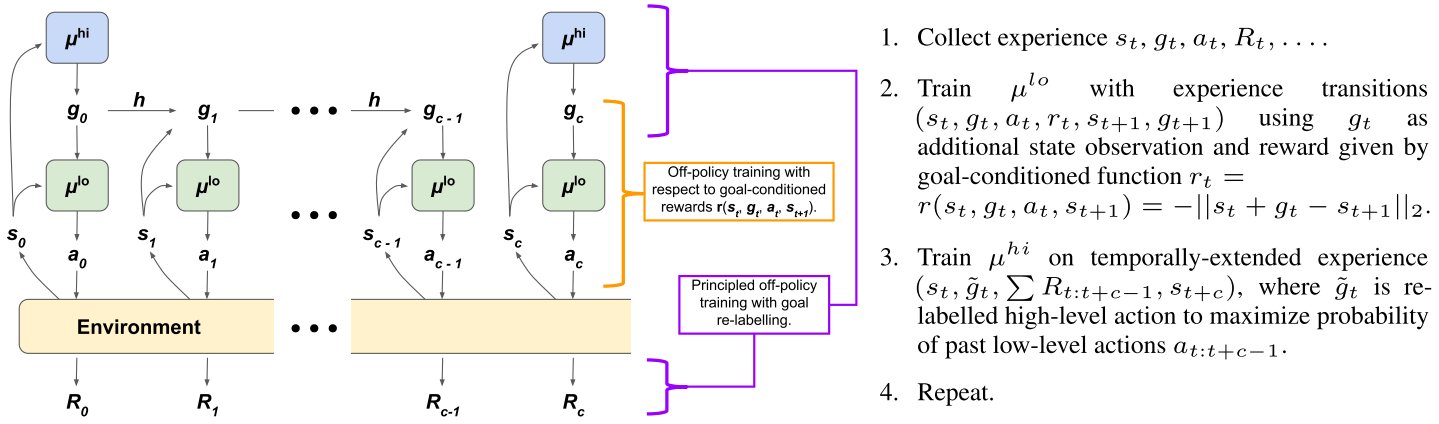
• [综合]

  1. 高层控制器构建较粗的抽象的目标给底层；

  2. 这些目标直接对应于底层控制器想要尝试去达到的states；

  3. 每一个timestep, 高层控制器使用由环境交互产生的state，并通过

     ​ ①每隔一段时间从高层控制器网络$\mu^{hi}$中进行采样($g_t\sim\mu^{hi}$)，或者

     ​ ②使用一个固定的目标转换函数$g_t=h(s_{t-1},g_{t-1},s_t)$

     等方式来生成high-level action(or goal) $g_t\in\mathbb{R}^{d_s}$；

  4. 对于上述产生的目标成为临时目标，每固定c步将进行重新采样；

  5. 底层控制器通过当前的状态及目标进行决策到仿真环境的动作$a_t \sim \mu^{lo}(s_t,g_t)$；

  6. 高层控制器使用一个固定的Parameterized reward function $r$ 向底层控制器提供一个内在的回报函数(intrinsic reward) $r_t=r(s_t,g_t,a_t,s_{t+_1})$；

  7. 底层策略将存储经验$(s_t,g_t,a_t,r_t,s_{t+1},h(s_t,g_t,s_{t+1}))$用于off-policy training；

  8. 高层控制器每隔c步获取环境回报$R_t$，存储高层状态转移序列$(s_{t:t+c-1},g_{t:t+c-1},a_{t:t+c-1},R_{t:t+c-1},s_{t+c})​$用于off-policy training。

---

三、具体策略

1. Parameterized reward function

   (1) 如何理解目标$g_t$

   ​ 高层控制器产生的Goal $g_t$ 意味着对于当前的观测状态的期望相对变化，即$g_t$代表着从当前$s_t$开始，底层控制器应该如何决策才能使得c步之后的$s_{t+c}$与$s_t+g_t$能够足够的接近。

   (2) 如何设计一个比较泛化的目标空间

   ​ 为了在不考虑状态变化的情况下保持目标的相同绝对位置，目标转换模型$h$定义为:

   $$h(s_t,g_t,s_{t+1})=s_t+g_t-s_{t+1}$$

   (3) 如何设计高层到底层的内在回报函数Parameterized reward function

   ​ 该回报函数通过定义当前状态与目标状态之间的欧式距离来表示:

   $$r(s_t,g_t,a_t,s_{t+1})=-||s_t+g_t-s_{t+1}||_2$$

   (4) 底层控制器的策略算法如何选择

   ​ 通过简单的将目标$g_t$加入观测元组的方式，使得底层框架可以使用强化学习的标准方法进行学习。

   ​ 比如使用DDPG那么loss就加入目标：

   $$L_{DDPG}=[(r(s_t,g_t,a_t,s_{t+1})+\gamma Q_\theta^{lo}(s_{t+1},g_{t+1},\mu_φ^{lo}(s_{t+1},g_{t+1})-Q_{\theta}^{lo}(s_t,g_t,a_t)]^2$$

   (5) 与以往工作的不同

   ​ Parameterized reward function 在之前的工作中也用过，但是他们用的时候目标都是间接通过表征学习给出的，而本文直接将目标当做一种预期的状态给到底层，更加直接。

2. 高层训练使用的Off-policy Correction

   (1)以往的工作大多基于on-policy ，这里引入了off-policy进行学习会带来怎样的问题

   ​ 引入off-policy的话，由于底层策略网络$\mu^{lo}$在当前和从replay buffer中采样的时候的策略网络是不同的，因而对于同一个目标，在前后两种策略网络下的状态转移序列是不同的。

   (2) 如何解决以上问题

   ​ 高层策略网络的状态转移序列为$(s_{t:t+c-1},g_{t:t+c-1},a_{t:t+c-1},R_{t:t+c-1},s_{t+c})$，我们将其转换为可以push到replay buffer中的state-action-reward 转移序列$(s_t,g_t\sum R_{t:t+c-1},s_{t+c})$，以兼容各种标准off-policy强化学习方法。

   ​ 更改$g_t$使其能够适应新的$\mu^{lo}$:

   • 先前的目标$g_t$诱导底层产生$a_{t:t+c−1} ∼ \mu^{lo}(s_{t:t+c−1}, g_{t:t+c−1})$行为。
   • 调整上述目标变成$\tilde {g_t}$使其能够诱导新的底层策略产生最大化概率：$\mu^{lo}(a_{t:t+c−1}|s_{t:t+c−1}, \tilde{g}_{t:t+c−1})$
   • $\tilde{g}$使用固定的目标转移函数$h$来得到

   (3) 如何获得新目标$\tilde{g}​$的最大化概率

   ​ 对于一般的强化学习算法而言策略的log概率可以表示为:

   $$log \mu^{lo}(a_{t:t+c−1}|s_{t:t+c−1}, \tilde{g}_{t:t+c−1}) ∝ −\frac{1}{2}\sum^{ t+c−1}_{i=t} ||a_i − \mu^{lo}(s_i, \tilde{g}_i)||_2^2 + const.$$

   ​ 这里文章通过离散采样的方式选择一个较大的值作为最大概率的估计，采样10个点为：

   • $g_t$

       * 按高斯分布在以$s_{t+c} − s_{t}​$为中心的分布上采样得到8个点
     
       * $s_{t+c} − s_t$
     

​