

一、摘要
二、先序工作
三、方法
3.1 Overview
(1)使用few-shot 方法解决非确定性环境下的连续自适应问题存在的问题:
agent必须从有限的过往经验中学习,并且这些过往经验是在没有环境变化下收集的。
(2)解决方法:
基于MAML进行构建,其中MAML (gradient-based model-agnostic meta-learning),在few-shot方法中效果较好。
本文从概率的角度对MAML在multi-task RF方向上进行扩展,并最终将其扩展到动态变化的任务中去。
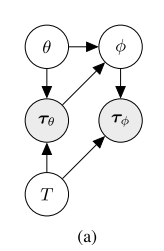
3.2 MAML的概率视角
2-1 定义
给定任务的分布 $D(T)$,对于每个任务$T$,$T$是一个如下的四元组
- $L_T$表示任务相关的Loss function,其将trajectory $\tau:=(x_0,a_1,x_1,R_1,…a_H,x_H,R_H)$与loss值进行映射;
- $P_T(x)$和$P_T(x_{t+1}|x_t,a_t)$定义了任务$T$中的马尔科夫决策过程;
- $H$表示任务的时间域(Horizon);
- $x_t$表示observations, $a_t$表示actions,
对于每个任务的Loss function $L_T$定义为:
2-2 Adaption Update
元学习的目标是找到一个过程,该过程能够通过在从$D(T) $采样的任务中获得有限经验的情况下,产生解决元学习问题的良好策略。具体为:
在使用策略$\pi_\theta$,从$D(T)$上采样了$K$个task $T \sim D(T)$,表示成$\tau_\theta^{1:K}$之后,构建一个新的针对采样出来的某个特定任务的策略$\pi_\phi$, 该策略的目标是在任务$T$上减小子序列的loss的期望 (expected subsequent loss)。
公式化上述描述即Adaption Update(Meta Upate)过程,MAML使用参数为$\theta$的$L_T$的梯度,构建了针对特定任务策略的参数$\phi$:
2-3 Meta Loss定义
Meta-Loss的定义如下:
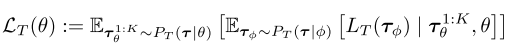
- 一般情况下,$\phi$从某种条件概率分布 $P_T(\phi|\theta, \tau_{1:k})$ 中生成, Meta Update公式等价于假设delta分布,即
2-4 Meta Loss优化
- 对于优化Meta-Loss,可以采用策略梯度的方法(TRPO,PPO等)按下述梯度进行优化。
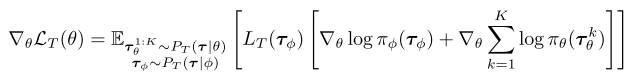
3.3 通过Meta-Learning实现连续自适应
在经典的多任务中,我们不假设任务的分布,$D(T)$。当环境是non-stationary时,可以把它看作是在某个时间尺度上的一系列stationary任务,其中任务对应于环境的不同动态。然后,$D(T)$由环境变化定义,任务将依赖于一定连续任务。因此,利用连续任务和meta-learn之间的依赖性,不断update policy,从而最大限度地减少与不断变化的环境交互过程中遇到的总loss期望。
例如,在Multi-agent中,当与不断优化自身策略的对手(例如,由于学习)进行比赛时,我们的agent应该理想地进行元学习,以预测更改并相应地更新其策略。
3-1 non-stationary的马尔科夫表示
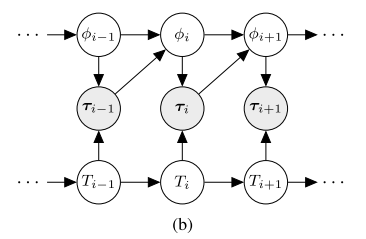
以概率的角度来描述non-stationary环境,该环境等价于上图所示的Markov 链表示的任务序列分布。 其目标是最小化某个长度$L$的马尔科夫任务序列上的loss期望。
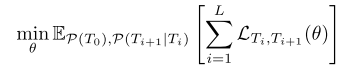
其中$P(T_0)$和$P(T_{i+1}|T_i)$表示初始概率及任务序列的马尔科夫链的概率转移。 值得注意的是,
(1)这里的动态马尔科夫链是二级层次化的,其中高层为任务的动态变化,下层为具体任务的MDP;
(2)目标$L_{T_i,T_{i+1}}$依赖于Meta learning过程定义的形式。
3-2 连续任务的Meta Loss定义
由于我们对任务间马尔可夫变换的最佳Adaption Update感兴趣,因此我们将一对连续任务的Meta Loss 定义如下:
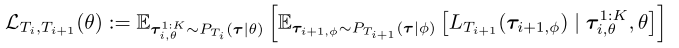
对于连续任务的Meta Loss与第二章定义的Meta Loss的不同之处在于:
(1) 连续任务的Meta Loss的trajectory $\tau_{i,\theta}^{1:K} $来自当前的任务$T_i$ , 并且用来构建Policy $\pi_\phi$ ,以便于执行下一个任务$T_{i+1}$;
(2) 虽然策略参数$\phi_i$是依赖于序列的,但是在上面连续任务的Meta Loss中一般初始参数设置为$\theta$。 P.S.(这是出于稳定性考虑。我们从经验上发现优化顺序更新$\phi_{i}$到$\phi_{i+1}$是不稳定的,通常倾向于发散,而从相同的初始化开始导致更好的行为。)
因此,优化$L_{T_i,T_{i + 1}}(θ)$ 相当于使用任务链中的单位滞后,截断随着时间的推移反向传播。
3-3 连续任务的Adaption Update
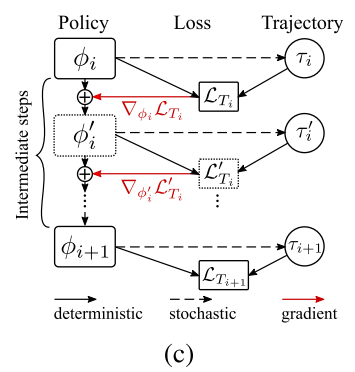
为了构建任务$T_{i+1}$的策略参数,我们从参数$\theta$开始,使用adaptive update进行多次 meta-gradient step。(假设step数是$M$,经验参考值为2~5次): 【原文中的公式(7)】
其中$\{\alpha_m\}^M_{m=1}$是meta-gradient step sizes 集合,其优化与$\theta$ 相关。 这部分的meta-update计算图如下图所示:
3-4 连续任务的Meta Loss优化
连续任务的Meta Loss优化和Meta Loss优化的形式基本相同,只是现在要同时考虑$T_i$和$T_{i+1}$的期望:【原文中的公式(8)】
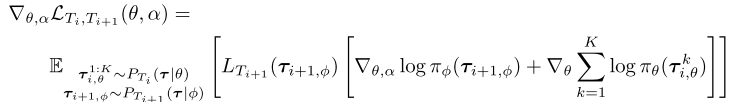
需要注意的是:
计算adaption update的时候需要在策略$\pi_\theta$下与环境进行交互并同时计算meta-loss。
3.4 训练过程中的Meta-Learning
当获得了一系列连续任务对的分布$P(T_{i-1},T_i)$之后,我们可以通过使用梯度方法,对参数$\theta$和$\alpha$同时优化来实现对 adaptation updates 的 meta learn。

Algorithm1: 在任务$T_{i+1}$中交互时,使用$\pi_\theta$ 策略从$T_i$和$\pi_\phi$收集 trajectory。(line 5)
直观地说,该算法搜索$θ$和$α$,这样根据$T_i$的轨迹计算出的adaptive update(参照原文公式(7)),产生一个策略$π_\phi$,这有助于对于求解$T_{i+1}$。这里的主要假设是,$T_i$的轨迹包含了一些关于$T_{i+1}$的信息。注意,将adaption steps 作为计算图(图c)的一部分,并通过整个图的反向传播来优化$θ$和$α$,这需要计算二阶导数。
3.5 执行过程中的自适应
为了在training过程中计算无偏自适应梯度,必须要使用策略$\pi_\theta $在任务$T_i$上收集经验。在test过程中,由于环境的不确定性,通常很难多次遇到同样的任务。因此,保持使用$\pi_\phi$进行决策,并且对每个新任务,reuse过往经验来计算更新参数$\phi$ (参考algorithm2):

为了修正过往经验的策略与当前的策略$\pi_\theta$的区别,使用重要性采样进行修正,在每一个单步meta update过程中,执行以下操作:【原文中的公式(9)】
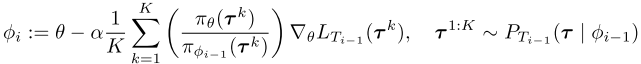
其中$\pi_{\phi_{i-1}}$和$\pi_{\phi_i}$分别用来从任务$T_{i-1}$和$T_{i}$中生成轨迹。对于公式(7)中的多步更新,直接将对应项按照公式(9)换成重要性采样就行了
