【确定性策略梯度类】 DPG,DDPG,TD3,D4PG

参考

【强化学习】确定性策略强化学习-DPG&DDPG算法推导及分析

Deep Reinforcement Learning - 1. DDPG原理和算法

一、确定性策略梯度

​ Deepmind的D.Silver等在2014年提出DPG： Deterministic Policy Gradient， 即确定性的行为策略，每一步的行为通过函数$μ$直接获得确定的值：

$$a_t=μ(s_t|θ_μ)$$

​ 这个函数$μ$即最优行为策略，不再是一个需要采样的随机策略。为何需要确定性的策略？简单来说，PG方法有以下缺陷：

​ 即使通过PG学习得到了随机策略之后，在每一步行为时，我们还需要对得到的最优策略概率分布进行采样，才能获得action的具体值；而action通常是高维的向量，比如25维、50维，在高维的action空间的频繁采样，无疑是很耗费计算能力的。在PG的学习过程中，每一步计算policy gradient都需要在整个action space进行积分:

$$\nabla_θ=∫_S∫_Aρ(s)π_θ(a|s)Q_π(s,a)dads$$

​ 这个积分我们一般通过Monte Carlo 采样来进行估算，需要在高维的action空间进行采样，耗费计算能力。如果采取简单的Greedy策略，即每一步求解$ argmax_a Q(s,a)$也不可行，因为在连续的、高维度的action空间，如果每一步都求全局最优解，太耗费计算性能。
​ 将DPG算法融合进actor-critic框架，结合Q-learning或者Gradient Q-learning这些传统的Q函数学习方法，经过训练得到一个确定性的最优行为策略函数。

二、DPG

DPG算法本身采用的是PG方法,且是Off-Policy方法(也可以是On-Policy)，因而直接对轨迹的价值回报进行求导。如下式求导，其中$\mu_\theta (s)$为生成确定性行动的策略函数。

$$\nabla_\theta v_{\mu_{\theta}} (s)=\nabla_\theta[q_\mu(s,\mu_\theta(s))]$$

根据链式法则，由于$\mu_\theta(s)$与确定性策略价值函数$q_\mu$有关,因而：

$$\nabla_\theta v_\mu(s) = \nabla_{\mu_\theta(s)}[q_\mu(s, \mu_\theta(s))]\nabla_\theta\mu_\theta(s)$$

由于是确定性策略，在价值函数$q(s,μ_\theta(s))$中有策略参数$\theta$，因此需要将价值函数对策略求导。

相较于随机策略梯度算法而言,如下是随机性策略梯度的目标函数梯度:

$$∇_θJ(θ)=\mathbb{E}_{τ∼π_θ}[(\sum_{t=0}^T∇_θ\logπ_θ(a_{i,t}∣s_{i,t}))(\sum_{t=0}^Tr(s_{i,t},a_{i,t}))]$$

在DPG这个梯度公式中，没有了与动作有关的期望项，因此相对于随机性策略，确定性策略需要的学习数据少，算法效率高，尤其对于动作空间维数很大的情况。

---

三、策略模型参数的一致性

​ 在DPG中为了更好地使用Off-policy,并使用TD降低方差，定义函数 $Q^\omega (s,a):S×A→R$ 用来拟合真实的状态动作值函数$\hat{Q}^\pi(s,a)$，如果$Q^\omega$收敛，那么L2范数梯度将满足如下公式:

$$\begin{aligned} \nabla_\omega Loss &∝ \nabla_\omega\mathbb{E}_{s,a}[\hat{Q}^\pi(s,a)-Q^\omega(s,a)]^2\\&= \mathbb{E}_{s,a\sim\tau}[(\hat{Q}^\pi(s,a)-Q^\omega(s,a))-\nabla _\omega Q^\omega(s,a)]\\&=0 \end{aligned}$$ $$\nabla_\omega Q^\omega(s,a)=\nabla_\theta\log\pi_\theta(s,a)=\nabla_\theta\pi_\theta(s,a)\frac{1}{\pi_\theta(s,a)}$$

​ 在计算梯度时可以使用$Q^ω:S×A→R $代替真实的动作状态值函数$Q(s,a) $。并且神经网络满足这个性质，因此可以使用神经网络拟合动作状态值函数。这样价值模型不需要遵循某个具体的策略，因此可以使用off-policy的方式进行学习更新。

---

四、DPG目标函数

• on-policy的确定性策略梯度算法

  

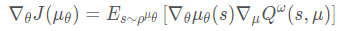
• off-policy的确定性策略梯度算法(Replay buffer中的数据是通过$\beta$采样得到的)

  

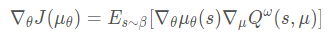
​ 上两式的区别就是使用了不同的数据采样分布。可以看到off-policy缺少了重要性采样，这是由于确定性策略的动作是固定值，不是一个分布；其次是因为确定性策略值函数的评估采用的是Q-learning的方法，即使用TD(0)估计动作值函数并忽略重要性权重，值函数不依赖于任何策略，并贪心获取下一个动作。

​ 这个$β$不是我们想要得到的最优策略，仅仅在训练过程中，生成下达给环境的action， 从而获得我们想要的数据集，比如状态转换(transitions)、或者agent的行走路径等，然后利用这个数据集去 训练策略$μ$，以获得最优策略。在test 和 evaluation时，使用$μ$，不会再使用$β$。

---

• [Actor]衡量一个策略网络的表现(策略网络目标函数)，最大化策略目标: (根据上面推导的DPG)

$$\begin{aligned} J_\beta (\theta)&=\int_S ρ^\beta(s)Q^\omega(s, \mu(s))ds\\ &=\mathbb{E}_{s\simρ^\beta}[Q^\omega(s, \mu(s))] \end{aligned}$$

​ $s$是环境的状态，这些状态(或者说agent在环境中走过的状态路径)是基于agent的behavior策略产生的，它们的分布函数(pdf) 为$ρ^β$；
​ $Q^\omega(s,μ(s))$ 是在每个状态下，如果都按照$μ$策略选择acton时，能够产生的$Q$值。 也即，$J_β(μ)$是在$s$根据$ρ^β$分布时，$Q^\omega(s,μ(s))​$ 的期望值。

• [Critic]最小化值网络目标:

  $$\hat{Q}^\omega(s_t, a_t)=\mathbb{E}[r(s_t,a_t)+\gamma Q^\omega(s_{t+1},a_{t+1})]$$ $$J_\beta(\omega)=\mathbb{E}_{s\simρ^\beta}[\frac{1}{2}(r_t+\gamma Q^\omega(s_{t+1},a_{t+1})-Q^\omega(s_t,a_t))^2]$$

最终DPG的目标函数为:（$\omega$是值网络(SGD优化)，$\theta$是策略网络(SGA优化)）

​

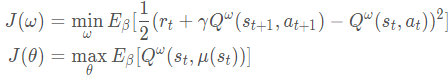
参数更新为：

---

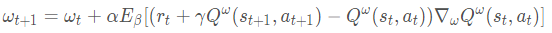
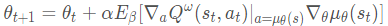
五、DDPG

DDPG借用了target net还有滑动平均方法更新behavior网络参数

其更新方法如下：

$$\begin{align} &\delta_t=r_t+\gamma Q^{\omega'}(s_{t+1},\mu_{\theta'}(s_{t+1}))-Q^\omega(s_t,a_t)\\ &\omega_{t+1} = \omega_t+\alpha_\omega \delta_t \nabla_\omega Q^\omega(s_t,a_t) \\ &\theta_{t+1} = \theta_t+\alpha_\theta \nabla_\theta\mu_\theta(s_t)\nabla_a Q^\omega(s_t,a_t)|_{a=\mu_\theta(s_t)} \\ &\theta'=\tau\theta+(1-\tau)\theta' \\ &\omega ' = \tau\omega+(1-\tau)\omega' \end{align}$$

对比一下DQN

六、TD3

参考：TD3

TD3(Twin Delayed Deep Deterministic policy gradient algorithm )主要对DDPG做了一些改进:

1. 引入DoubleDQN的思想，来消除过拟合问题(两个Critic, 一个Actor)

   DoubleDQN中使用Current Net（Behavior net）来代替TargetNet，以减小Bias。

   $$y_j = r_{j+1}+\gamma Q(s_{j+1},argmax_{a'}Q(s_{j+1},a';\theta);\theta^-)$$

   映射到DPG过程中,其中$\pi_φ(s’)$是CurrentNet:

   $$y = r + \gamma Q_\theta(s',\pi_φ(s'))$$

   即critic用更新较慢的target network，actor还是更新快的；但由于本身actor更新也不快，所以没啥效果。

   如果类比double Q-learning，使用两个actor、两个critic写出来的更新目标为

   

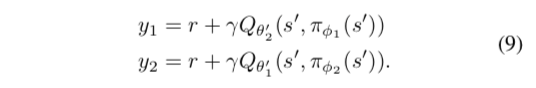
   本着“宁可低估，也不要高估”的想法（因为actor会选择高的，因此高估的会累积起来），再把目标改写成

   

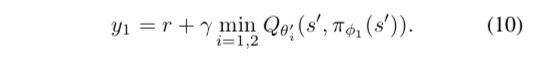
   最后发现两个actor也没啥用，就用一个actor，这个actor根据 $Q_{\theta_1}​$ 来更新。两个critic的更新目标都是一样的，即 $y_2 = y_1​$ 。这样的算法相比于改变之前的就等于多了一个和原来critic同步更新的辅助critic $Q_{\theta_2} ​$，在更新target的时候用来取min。

2. 使用TargetNet

   实验结果表明，当policy固定不变的时候，是否使用target network其价值函数都能最后收敛到正确的值；但是actor和critic同步训练的时候，不用target network可能使得训练不稳定或者发散。因此算法的中critic的更新目标都由target network计算出来

   

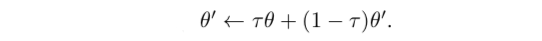
   并且，价值函数估计准确之后再来更新policy会更好，因此采用了delayed policy update，即以较高的频率更新价值函数，以较低的频率更新policy。

3. 使用Target Policy 平滑正则

   希望学到的价值函数在action的维度上更平滑，因此价值函数的更新目标每次都在action上加一个小扰动

   

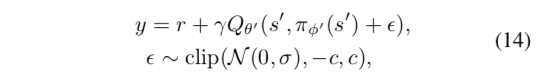
七、D4PG

论文 DISTRIBUTED DISTRIBUTIONAL DETERMINISTIC
POLICY GRADIENTS

总体框架与DDPG相同，引入了一些trick：

1. 支持分布式，由于是off-policy的算法，因此可以使用多个actor去分布式地采样，然后存储在同一个replay buffer中，learner从buffer中采样，更新之后再将权重同步到各个actor上

2. critic使用价值函数分布，损失函数变为(d是距离度量)：

   $$L(w)=\mathbb{E}_ρ[d(\Tau_{\pi_{\theta'}}Z_{\omega'}(x,a),Z_\omega(x,a))]$$

   其中$(T_\pi Z)(x, a)=r(x,a)+\gamma\mathbb{E}[Z(x’,\pi(x’))|x,a]$ 为 distributional Bellman operator, $Z$是用来估计Q的， $Q_\pi(x,a) = \mathbb{E}Z_\pi(x,a)$

3. 引入n-step TD error：这样可以减少更新的variance

4. 使用prioritized experience replay：可以加速学习