生成对抗网络(笔记)

参考

1. 令人拍案叫绝的Wasserstein GAN
2. WGAN最新进展：从weight clipping到gradient penalty
3. Ten paper: GAN-GP(Gradient Penalty)
4. 深度有趣 | 16 令人拍案叫绝的WGAN
5. 开发者自述：我是这样学习 GAN 的
6. 推荐：生成对抗网络综述

一、 基本概念

1. 符号定义

   $D$ 判别模型， $G$ 生成模型

   $x​$ 数据集中的数据分布，$z​$ 某种随机分布

2. 目标函数（详细参见第四部分）(找一系列D让其对应的V最大，然后在这些最大的V里面选一个最小的)

   $$min_Gmax_DV(G,D)=\mathbb{E}_x[log(D(x))]+\mathbb{E}_z[log(1-D(G(z)))]$$

   • D Loss (MC采样，相当于训练二分类器$x \sim P_{data}$一类，$\hat{x} \sim G(z)$一类):

     $$max_DV(G,D)=\mathbb{E}_x[log(D(x))]+\mathbb{E}_z[log(1-D(G(z)))]$$

   • G Loss原始 （MiniMax GAN[MMGAN]）(判别器越好，生成器梯度消失越严重)

     $$\mathbb{E}{_{x\sim P_g}}[log(1-D(x))]$$

   • G Loss改进 (Non-saturating GAN[NSGAN] )(-log trick) (其实与原始的差别不大)

     $$\mathbb{E}{_{x\sim P_g}}[-log(D(x))]$$

3. 释义

   $G$的目标是最大化生成数据与数据集数据的似然，减小生成数据与数据集数据之间的差距（原始GAN就是JSD）。对于生成器$ G $来说，为了尽可能欺骗$ D$，所以需要最大化生成样本的判别概率 $D(G(z))$，即最小化$ log(1-D(G(z)))$，注意：$log(D(x)) $一项与生成器$ G $无关，所以可以忽略。

   $$G^{*}=argmin_G(Divergence(P_G,P_{data}))=argmin_G max_DV(D,G)$$

   $D$要解决的问题是一个二分类问题，$V(D,G)$ 为二分类问题中常见的交叉熵损失。

   $$D^{*}=argmax_DV(D,G)\\ V(D,G) = \mathbb{E}_{x\sim P_{data}}[logD(x)]+\mathbb{E}_{x \sim P_G}[1-log(1-D(x))]$$

二、 原理推导

参考: 开发者自述：我是这样学习 GAN 的

​ 真实数据的分布$ P_{data}(x)$，$x$ 是一个真实数据，是一个向量，这个向量集合的分布就是 $P_{data}$。我们需要生成一些也在这个分布内的数据，如果直接就是这个分布的话，怕是做不到的。

​ 现有的 Generator 生成的分布可以假设为 $P_G(x;θ)$，这是一个由 $ θ $ 控制的分布，$θ$ 是这个分布的参数（如果是高斯混合模型，那么 $ θ$ 就是每个高斯分布的均值和方差) 。

​ 假设我们在真实分布中取出一些数据，${x_1, x_2, … , x_m}$，我们想要计算一个似然 $P_G(x_i; θ)$。

​ 对于这些数据，在生成模型中的似然就是

$$L=\prod_{i=1}^mP_G(x^i;\theta)$$

1. GAN原理

   最大化上面这个似然，等价于让 Generator 生成那些真实数据分布的概率最大。这就变成了一个最大似然估计的问题了，我们需要找到一个 $θ^*$ 来最大化这个似然。(倒数第三行减掉的$P_{data}$项是为了凑KL，其不包含G的参数相关项，没有影响单调性。)

   

   固定$G$,求一个最优的$D^*​$

   $$\begin{aligned} V&=\mathbb{E}_{x\sim P_{data}}[logD(x)]+\mathbb{E}_{x\sim P_G}[log(1-D(x))]\\ &=\int_x P_{data}(x)\log D(x)dx+\int_xP_G(x)\log (1-D(x))dx \\ &=\int_x[P_{data}(x)\log D(x)+P_G(x)\log(1-D(x))]dx \end{aligned}$$

   那么转为优化$f(D) = P_{data}(x)\log D(x)+P_G(x)\log(1-D(x))$

   对$f(D)$求偏导:

   $$\frac{df(D)}{dD} = P_{data}(x)×\frac{1}{D}+P_G(x)×\frac{1}{1-D}×(-1) = 0$$

   可以解得:

   $$D^*(x) = \frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$$

   对于一个给定的 x，得到最优的 D 如上图，范围在 (0,1) 内，把最优的 $D^{*} ​$ 带入V

   $$\begin{aligned} &max_DV(G,D)&=V(G,D^*)\\ &=\mathbb{E}_{x\sim P_{data}}[logD^*(x)]+\mathbb{E}_{x\sim P_G}[log(1-D^*(x))]\\ &=\mathbb{E}_{x\sim P_{data}}[log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}]+\mathbb{E}_{x\sim P_G}[log(1-\frac{P_{G}(x)}{P_{data}(x)+P_G(x)})] \\ &=\int_xP_{data}(x)log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}dx+\int_xP_G(x)log(1-\frac{P_{G}(x)}{P_{data}(x)+P_G(x)})dx\\ &=-2log2+\int_xP_{data}(x)log\frac{P_{data}(x)}{(P_{data}(x)+P_G(x))/2}dx+\int_xP_G(x)log(1-\frac{P_{G}(x)}{(P_{data}(x)+P_G(x))/2})dx \\ &=-2log2+KL(P_{data}(x)||\frac{P_{data}(x)+P_G(x)}{2})+KL(P_G(x)||\frac{P_{data}+P_G(x)}{2}) \\ &= -2log2+2JSD(P_{data}(x)||P_G(x)) \end{aligned}$$

   所以最终(V(G,D)可以看成是JSD)

   $$\mathbb{E}_{x\sim P_r}[\log D^*(x)] + \mathbb{E}_{x\sim P_g}[\log(1-D^*(x))] = 2JS(P_r || P_g) - 2\log 2$$

   表示两个分布之间的差异，最小值是$ -2log2​$，最大值为 $0​$。观察上式，当 $P_G(x)=P_{data}(x)​$ 时，G 是最优的。

三、GAN的训练

有了上面推导的基础之后，我们就可以开始训练 GAN 了。结合我们开头说的，两个网络交替训练，我们可以在起初有一个 $G_0$ 和 $D_0$，先用Gradient Ascent训练 $D_0$ 找到 ：

然后固定 $D_0​$ 开始训练 $G_0​$， 训练的过程都可以使用 gradient descent，以此类推，训练 $D_1,G_1,D_2,G_2,…​$

但是这里有个问题就是，你可能在 $D_0^*​$ 的位置取到了：

然后更新 $G_0$ 为 $G_1​$，可能会出现：

但是并不保证会出现一个新的点$ D_1^*$ 使得：

这样更新 $G$ 就没达到它原来应该要的效果，如下图所示(G变化太大导致的JS值不稳定)：

避免上述情况的方法就是更新 $G ​$的时候，不要更新 $G ​$太多。

知道了网络的训练顺序，我们还需要设定两个 loss function，一个是$ D$ 的 loss，一个是 $G$ 的 loss。下面是整个 GAN 的训练具体步骤：

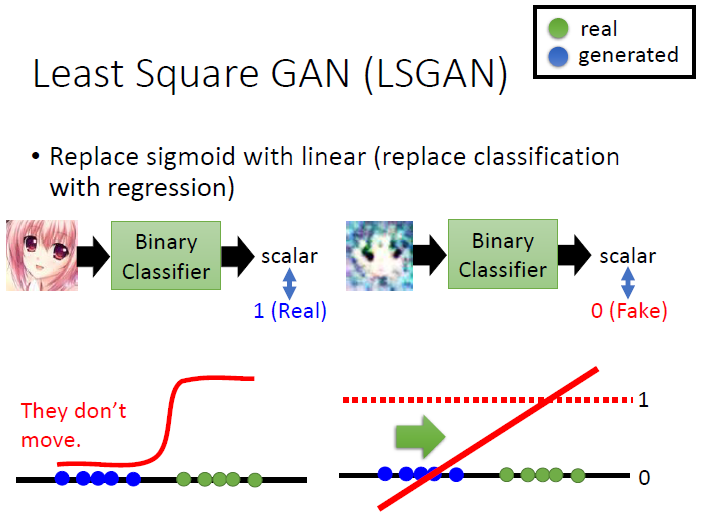
​ 适当多练D，少练G以免G的变化过大，导致JS大小不稳定，在原始GAN中，D也不要练太多，原始GAN的D是一个二分类器，用sigmoid激活，如果练的太多，导致分布很难继续拟合，形象的说就是土推不动，这块儿可以用 Least square GAN来解决，参见下面这张图(来自李宏毅老师的教程。

四、存在的问题

1. G的Loss function收敛速度问题：

   $G​$ 的 loss function $\mathbb{E}{_{x\sim P_g}}[log(1-D(x))]​$ 还是有一点小问题，下图是两个函数的图像：

​ [问题原因] $log(1-D(x)) $是我们计算时 G 的 loss function，但是我们发现，在$ D(x) $接近于 0 的时候，这个函数十分平滑，梯度非常的小。这就会导致，在训练的初期，$G $想要骗过 $D$，变化十分的缓慢，而上面的函数，趋势和下面的是一样的，都是递减的。但是它的优势是在 $D(x) $接近 0 的时候，梯度很大，有利于训练，在 $D(x) $越来越大之后，梯度减小，这也很符合实际，在初期应该训练速度更快，到后期速度减慢。

​ [解决方案] 所以我们把$ G$ 的 loss function 修改为:

$$minimizeV=-\frac{1}{m}\sum_{i=1}^m \log(D(x^i))$$

1. Loss 没有变化，一直都是平的

   [问题] 此时$max_DV(G,D)=0$, $JS=log2$, $P_G$和$P_{data}$由于$D$过拟合导致完全没有交集，但是实际上两个分布是有交集的，造成这个的原因是因为，我们无法真正计算期望和积分，只能使用 sample 的方法，如果训练的过拟合了，D 还是能够完全把两部分的点分开:

   

   [问题原因] 对于这个问题，我们是否应该让 $D$变得弱一点，减弱它的分类能力，但是从理论上讲，为了让它能够有效的区分真假图片，我们又希望它能够，所以这里就产生了矛盾。

   还有可能的原因是，虽然两个分布都是高维的，但是两个分布都十分的窄，可能交集相当小，这样也会导致 JS divergence 算出来为$log2$，约等于没有交集。

   [解决方案] 解决的一些方法，有添加噪声，让两个分布变得更宽，可能可以增大它们的交集，这样 JS divergence 就可以计算，但是随着时间变化，噪声需要逐渐变小，换一种距离计算方法比如使用Wasserstein

2. Mode Collapse

   Mode collapse的出现应该可以说是必然的，其通过不同的散度进行拟合，最优的情况很可能就是出现在某一个密度较高的分布峰上。结局mode collapse的方法可以使用ensemble的方式，我这边还尝试过先聚类后gan的方式。