Hybrid A* 路径规划

发表于 | 更新于 | 评论数：
本文字数： 34k | 阅读时长 ≈ 31 分钟

参考:

Hybrid A Star 路径规划

Hybrid A* Path Planner for the KTH Research Concept Vehicle

分层有限状态机和无人车行为规划

[PAPER] : Path Planning in Unstructured Environments

Hybrid A* 的使用场景

​ 在斯坦福大学2007年参加的DARPA无人车城市挑战赛时使用的Junior，其在行为规划层提出了分层有限状态机的方式，如下图所示。

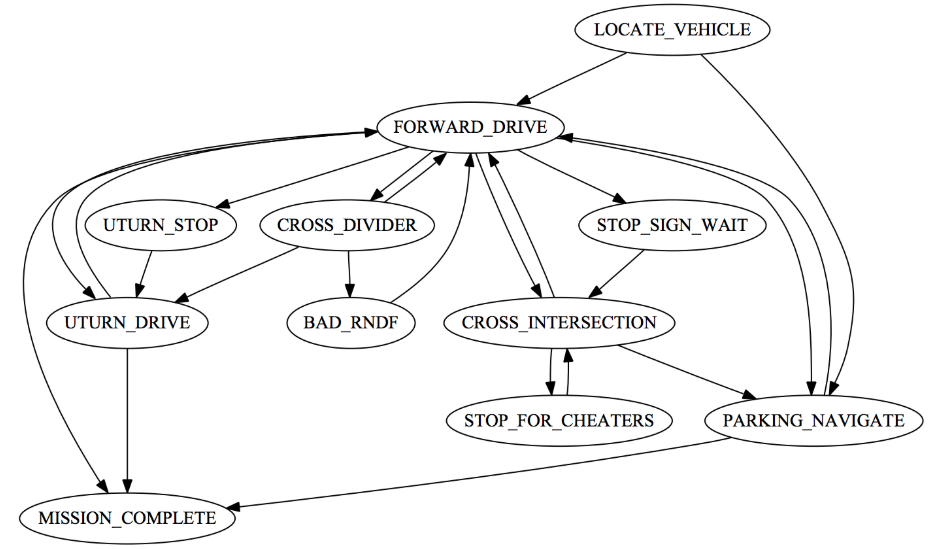
​ 其中，BAD_RNDF状态表示的是，当前道路与系统的路网图不同的时候，无人车将采用Hybrid A*来进行规划路径。

Hybrid A 与 A

Hybrid A* 的主要特点是：

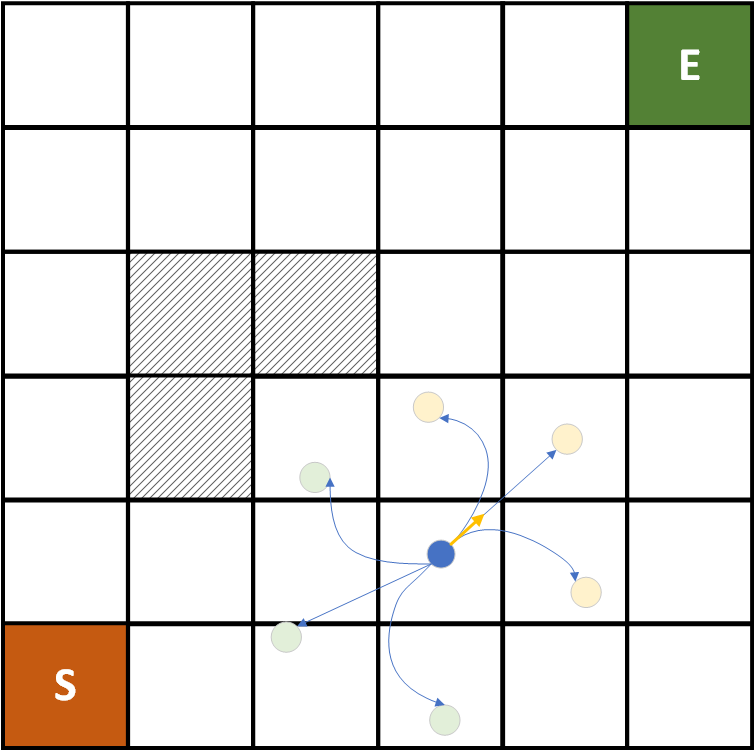
  • 考虑物体的实际运动方向约束，不像A*假定所有的相邻节点都可以顺利转移
  • A 的物体总是出现在栅格中心，而 Hybrid A 则不一定
  • Hybrid A* 是连续路径
  • Hybrid A 基于A

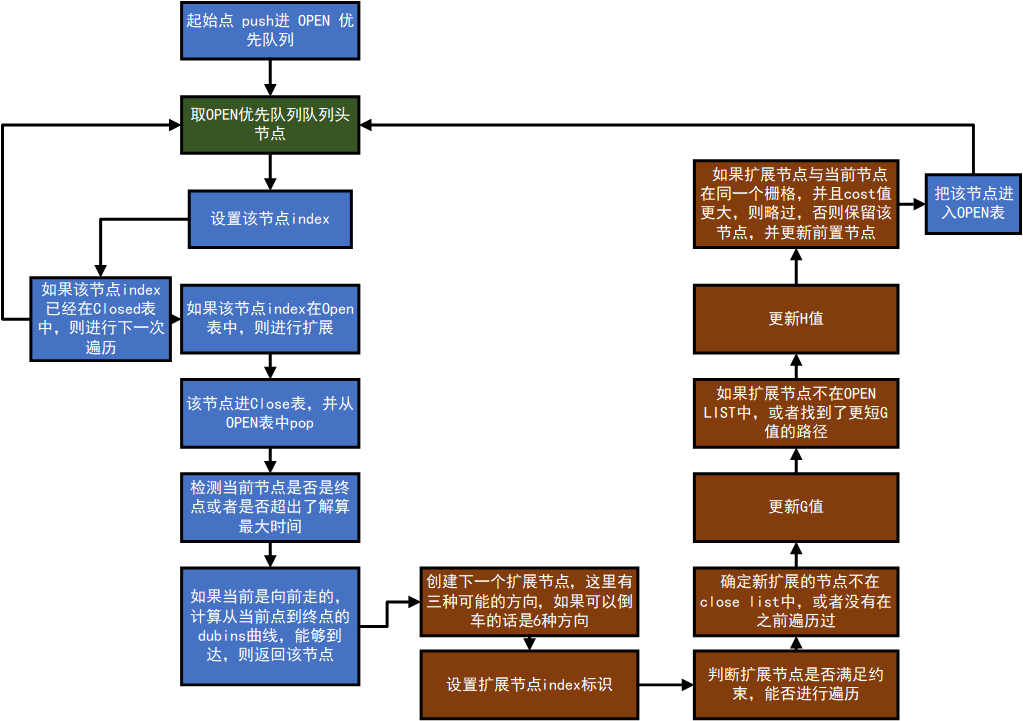
算法流程:

主要流程如下图所示，需要说明的是：

​ 算法考虑了车辆的x,y坐标，偏航角。

  1. G值更新策略如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    //###################################################
    //                                      MOVEMENT COST
    //###################################################
    void Node3D::updateG() {
      // 前向行驶
      if (prim < 3) {
        // penalize turning 当前一个节点的prim与当前节点的prim不相等时，判断发生偏转。
        if (pred->prim != prim) {
          // 方向变化
          if (pred->prim > 2) {
            g += dx[0] * Constants::penaltyTurning * Constants::penaltyCOD;
          } else {
            g += dx[0] * Constants::penaltyTurning;
          }
        } else {
          g += dx[0];
        }
      }
      // 倒车行驶
      else {
        // penalize turning and reversing
        if (pred->prim != prim) {
          // penalize change of direction
          if (pred->prim < 3) {
            g += dx[0] * Constants::penaltyTurning * Constants::penaltyReversing * Constants::penaltyCOD;
          } else {
            g += dx[0] * Constants::penaltyTurning * Constants::penaltyReversing;
          }
        } else {
          g += dx[0] * Constants::penaltyReversing;
        }
      }
    }

  1. H值更新策略如下：

    可以支持倒车时计算当前节点到终点的Reeds-Shepp 曲线，仅支持前向行驶时计算Dubins曲线；

    H值为Reeds-Shepp曲线、Dubins曲线、曼哈顿距离三种cost解算出来的最大值。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    //###################################################
    //                                         COST TO GO
    //###################################################
    void updateH(Node3D& start, const Node3D& goal, Node2D* nodes2D, float* dubinsLookup, int width, int height, CollisionDetection& configurationSpace, Visualize& visualization) {
      float dubinsCost = 0;
      float reedsSheppCost = 0;
      float twoDCost = 0;
      float twoDoffset = 0;

      // if dubins heuristic is activated calculate the shortest path
      // constrained without obstacles
      if (Constants::dubins) {
        ompl::base::DubinsStateSpace dubinsPath(Constants::r);
        State* dbStart = (State*)dubinsPath.allocState();
        State* dbEnd = (State*)dubinsPath.allocState();
        dbStart->setXY(start.getX(), start.getY());
        dbStart->setYaw(start.getT());
        dbEnd->setXY(goal.getX(), goal.getY());
        dbEnd->setYaw(goal.getT());
        dubinsCost = dubinsPath.distance(dbStart, dbEnd);
      }

      // if reversing is active use a
      if (Constants::reverse && !Constants::dubins) {
        //    ros::Time t0 = ros::Time::now();
        ompl::base::ReedsSheppStateSpace reedsSheppPath(Constants::r);
        State* rsStart = (State*)reedsSheppPath.allocState();
        State* rsEnd = (State*)reedsSheppPath.allocState();
        rsStart->setXY(start.getX(), start.getY());
        rsStart->setYaw(start.getT());
        rsEnd->setXY(goal.getX(), goal.getY());
        rsEnd->setYaw(goal.getT());
        reedsSheppCost = reedsSheppPath.distance(rsStart, rsEnd);
        //    ros::Time t1 = ros::Time::now();
        //    ros::Duration d(t1 - t0);
        //    std::cout << "calculated Reed-Sheep Heuristic in ms: " << d * 1000 << std::endl;
      }

      // if twoD heuristic is activated determine shortest path
      // unconstrained with obstacles
      if (Constants::twoD && !nodes2D[(int)start.getY() * width + (int)start.getX()].isDiscovered()) {
        //    ros::Time t0 = ros::Time::now();
        // create a 2d start node
        Node2D start2d(start.getX(), start.getY(), 0, 0, nullptr);
        // create a 2d goal node
        Node2D goal2d(goal.getX(), goal.getY(), 0, 0, nullptr);
        // run 2d astar and return the cost of the cheapest path for that node
        nodes2D[(int)start.getY() * width + (int)start.getX()].setG(aStar(goal2d, start2d, nodes2D, width, height, configurationSpace, visualization));
      }

      if (Constants::twoD) {
        // offset for same node in cell
        twoDoffset = sqrt(((start.getX() - (long)start.getX()) - (goal.getX() - (long)goal.getX())) * ((start.getX() - (long)start.getX()) - (goal.getX() - (long)goal.getX())) +
                          ((start.getY() - (long)start.getY()) - (goal.getY() - (long)goal.getY())) * ((start.getY() - (long)start.getY()) - (goal.getY() - (long)goal.getY())));
        twoDCost = nodes2D[(int)start.getY() * width + (int)start.getX()].getG() - twoDoffset;

      }

      // return the maximum of the heuristics, making the heuristic admissable
      start.setH(std::max(reedsSheppCost, std::max(dubinsCost, twoDCost)));
    }

代码

参考：Hybrid A* Path Planner for the KTH Research Concept Vehicle 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
//###################################################
//                                        3D A*
//###################################################
Node3D* Algorithm::hybridAStar(Node3D& start,
                               const Node3D& goal,
                               Node3D* nodes3D,
                               Node2D* nodes2D,
                               int width,
                               int height,
                               CollisionDetection& configurationSpace,
                               float* dubinsLookup,
                               Visualize& visualization) {

  // PREDECESSOR AND SUCCESSOR INDEX
  int iPred, iSucc;
  float newG;
  // Number of possible directions, 3 for forward driving and an additional 3 for reversing
  int dir = Constants::reverse ? 6 : 3;
  // Number of iterations the algorithm has run for stopping based on Constants::iterations
  int iterations = 0;

  // VISUALIZATION DELAY
  ros::Duration d(0.003);

  // OPEN LIST AS BOOST IMPLEMENTATION
  typedef boost::heap::binomial_heap<Node3D*,
          boost::heap::compare<CompareNodes>
          > priorityQueue;
  priorityQueue O;  // OPEN_LIST 优先队列
  
  // update h value
  updateH(start, goal, nodes2D, dubinsLookup, width, height, configurationSpace, visualization);
  // mark start as open
  start.open();
  // push on priority queue aka open list
  O.push(&start);
  iPred = start.setIdx(width, height);
  nodes3D[iPred] = start;

  // NODE POINTER
  Node3D* nPred;
  Node3D* nSucc;

  // float max = 0.f;

  // continue until O empty
  while (!O.empty()) {

    // pop node with lowest cost from priority queue
    nPred = O.top();
    // set index
    iPred = nPred->setIdx(width, height);
    iterations++;

    // RViz visualization
    if (Constants::visualization) {
      visualization.publishNode3DPoses(*nPred);
      visualization.publishNode3DPose(*nPred);
      d.sleep();
    }

    // _____________________________
    // LAZY DELETION of rewired node
    // if there exists a pointer this node has already been expanded
    if (nodes3D[iPred].isClosed()) {
      // pop node from the open list and start with a fresh node
      O.pop();
      continue;
    } 
    // _________________
    // EXPANSION OF NODE
    else if (nodes3D[iPred].isOpen()) {
      // add node to closed list
      nodes3D[iPred].close();
      // remove node from open list
      O.pop();

      // _________
      // GOAL TEST 检测当前节点是否是终点或者是否超出了解算最大时间
      if (*nPred == goal || iterations > Constants::iterations) {
        // DEBUG
        return nPred;
      }

      // ____________________
      // CONTINUE WITH SEARCH
      else {
        // _______________________
        // SEARCH WITH DUBINS SHOT
        if (Constants::dubinsShot && nPred->isInRange(goal) && nPred->getPrim() < 3) {
          nSucc = dubinsShot(*nPred, goal, configurationSpace);

          if (nSucc != nullptr && *nSucc == goal) {
            //DEBUG
            // std::cout << "max diff " << max << std::endl;
            return nSucc;
          }
        }

        // ______________________________
        // SEARCH WITH FORWARD SIMULATION
        for (int i = 0; i < dir; i++) {
          // 创建下一个扩展节点，这里有三种可能的方向，如果可以倒车的话是6种方向
          nSucc = nPred->createSuccessor(i);
          // 设置节点遍历标识
          iSucc = nSucc->setIdx(width, height);

          // 判断扩展节点是否满足约束，能否进行遍历
          if (nSucc->isOnGrid(width, height) && configurationSpace.isTraversable(nSucc)) {

            // 确定新扩展的节点不在close list中，或者没有在之前遍历过
            if (!nodes3D[iSucc].isClosed() || iPred == iSucc) {

              // 更新G值
              nSucc->updateG();
              newG = nSucc->getG();

              // 如果扩展节点不在OPEN LIST中，或者找到了更短G值的路径
              if (!nodes3D[iSucc].isOpen() || newG < nodes3D[iSucc].getG() || iPred == iSucc) {

                // calculate H value
                updateH(*nSucc, goal, nodes2D, dubinsLookup, width, height, configurationSpace, visualization);

                // if the successor is in the same cell but the C value is larger 如果扩展节点与当前节点在同一个栅格，并且cost值更大，则略过
                if (iPred == iSucc && nSucc->getC() > nPred->getC() + Constants::tieBreaker) {
                  delete nSucc;
                  continue;
                }
                // if successor is in the same cell and the C value is lower, set predecessor to predecessor of predecessor
                else if (iPred == iSucc && nSucc->getC() <= nPred->getC() + Constants::tieBreaker) {
                  nSucc->setPred(nPred->getPred());
                }

                if (nSucc->getPred() == nSucc) {
                  std::cout << "looping";
                }

                // put successor on open list
                nSucc->open();
                nodes3D[iSucc] = *nSucc;
                O.push(&nodes3D[iSucc]);
                delete nSucc;
              } else { delete nSucc; }
            } else { delete nSucc; }
          } else { delete nSucc; }
        }
      }
    }
  }

  if (O.empty()) {
    return nullptr;
  }

  return nullptr;
}

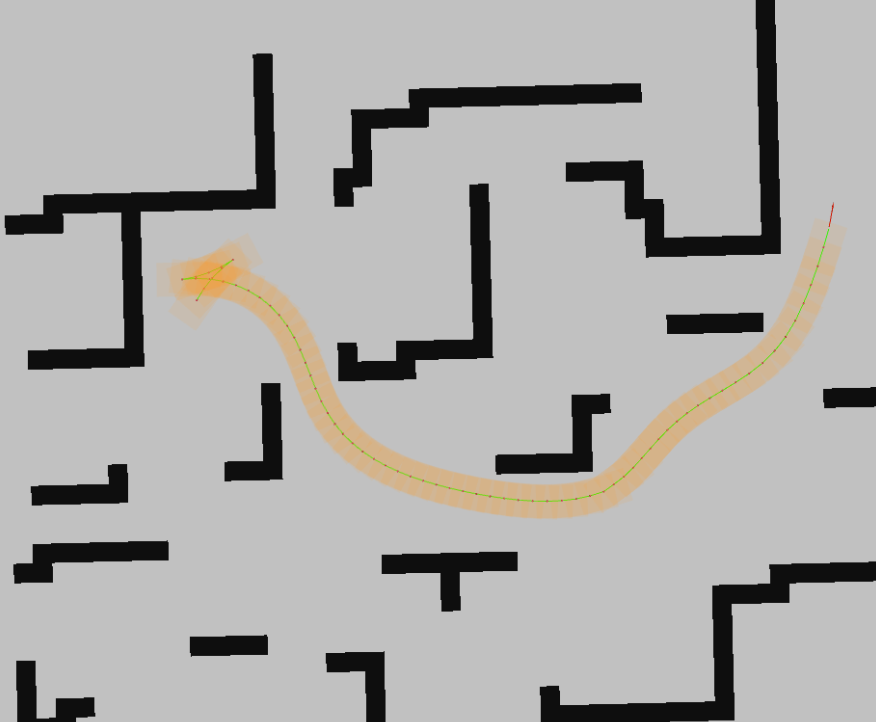
Rviz实验效果

本文标题:Hybrid A* 路径规划

文章作者:zhkmxx930

发布时间:2019年03月01日 - 16:03

最后更新:2019年03月05日 - 22:03

原始链接:https://zhkmxx9302013.github.io/post/c0e17f81.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

一分钱也是爱，mua~