强化学习专题笔记(一) 强化学习基础

一、长期回报

对于问题的简化，采用理想的MDP，简化问题到具有马尔科夫性，对于马尔科夫决策过程而言，在理想状态下，每一个行动都要为最终的目标最大化长期回报 而努力。

$\max\sum_{t}{r_t}$

但是很多情况下，仿真的时间维度较大，步数较多，甚至可以无限循环下去，这样的情况下我们需要引入一个可以和收敛的无穷数列，来替代我们最原始的长期回报公式。即对未来的回报乘以一个折扣率，使得长期回报变得更有意义：

$\sum_{t=0}{\gamma^tr_t} （\gamma < 1）$

由此我们引出长期回报的概念，即从当前状态开始对之后的所有回报，运用上式进行累加的折扣率计算：

$Ret_t=\sum_{k=0}\gamma^kr_{t+k+1}$

但是长期回报需要知道未来的行动情况，我们需要对上式进行一个合理的估计，因而我们定义了策略的价值。

二、值函数

由于环境的原因，MDP中的状态转移概率有时候并不能够确定，因而需要基于状态转移来估计长期回报的期望。τ是从某个状态s出发，根据策略与状态转移概率采样得到的序列(trajectory)。那么价值函数可以表示为：

$v_{\pi}{(s_t)} = \mathbb{E}_{s,a\simτ}[\sum_{k=0}\gamma^kr_{t+k+1}] =\sum_{\tau}{p(\tau)}{\sum_{k=0}^{\infin}{\gamma^k}{r_{t+k+1}}}$

根据MDP模型的形式，值函数一般分为两种：

状态值函数 $v_{\pi}{(s)}$: 已知当前状态s，按照某种策略行动产生的长期回报期望；
状态-动作值函数 $q_{\pi}{(s,a)}$: 已知当前状态s及动作a，按照某种策略行动产生的长期回报期望。

由于符合马尔科夫性，我们可以将值函数的形式进行马尔科夫展开,其中${\pi(a_t|s_t)}$表示，在$s_t$状态下选择策略$\pi$的概率，策略$\pi$将产生行动$a_t$，$p(s_{t+1}|s_t,a_t)$表示在策略$\pi$的情况下，从$s_t，a_t$到达$s_{t+1}$的概率。

$v_{\pi}{(s_t)}=\sum_{(s_t,a_t,...)\sim\tau}{\pi(a_t|s_t)}p(s_{t+1}|s_t,a_t)...{\sum_{k=0}^{\infin}{\gamma^k}{r_{t+k+1}}}$

三、贝尔曼方程

状态值函数的贝尔曼方程

通过代换消元，可以将上式整理为状态值函数的贝尔曼方程：

$v_{\pi}(s_t)=\sum_{a_t}\pi(a_t|s_t)\sum_{s_{t+1}}{p(s_{t+1}|s_t,a_t)[r_{t+1}+\gamma v_{\pi}(s_{t+1})]}$

更直观一点可以将贝尔曼方程描述为一种DP的形式，即当前状态$s$下，选择策略$\pi$的长期回报期望。

$v_{\pi}(s_t)=\sum_{a_t,s_t+1}\pi{(a_t|s_t)}\mathbb{E}[r_{t+1} + \gamma v_{\pi}(s_{t+1})]$

按Sutton的书表示：

$v_π(s)=\mathbb{E}_π[r_{t+1}+γv_π(s_{t+1})|s_t=s]$

状态-动作值函数的贝尔曼方程

类似地，可以定义状态-动作值函数的贝尔曼方程：

$q_{\pi}(s_t,a_t)=\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)\sum_{a_{t+1}}p(a_{t+1}|s_{t+1})[r_{t+1}+\gamma q_\pi{(s_{t+1},a_{t+1})}]$

按Sutton的书表示:

$q_\pi(s, a)=\mathbb{E}[r_{t+1} +\gamma q_{\pi}(s_{t+1}, a_{t+1})|s_{t}=s,a_{t}=a]$

Bellman optimality equation

$v_*(s)=\mathbb{E}[r_{t+1} +\gamma max_\pi{v(s_{t+1})|s_t=s}]$ $q_*(s,a)=\mathbb{E}[r_{t+1} +\gamma max_{a_{t+1}}{q(s_{t+1},a_{t+1})|s_t=s,a_t=a}]$

四、Monte-Carlo与Time Difference

MC 方差较大，需要较深的探索获取回报
TD 方差较小，偏差较大，可设定探索深度(1-step, n-step), Q-Learning, SARSA都属于TD

【参考】https://zhuanlan.zhihu.com/p/25239682

Monte-Carlo method适用于“情节式任务”（情节任务序列有终点，与“情节式任务”相对应的是“连续型任务”）。$Q(s,a)$就是整个序列的期望回报。MC增量更新中的Monte-Carlo error ($R-Q(s_t,a_t)$)：

$Q(s_t,a_t)\Leftarrow Q(s_t,a_t) + \alpha(R-Q(s_t,a_t))$

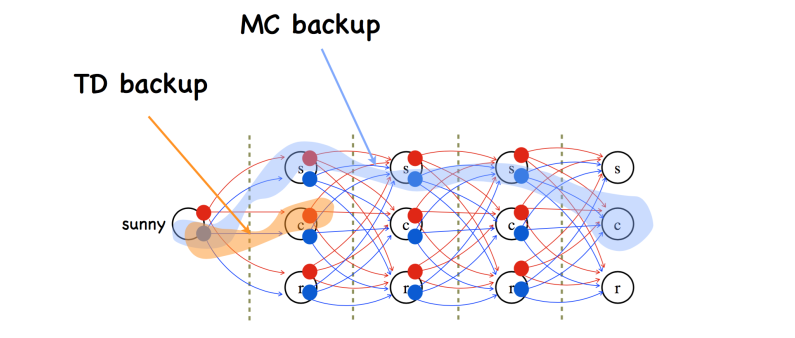
TD（Time Difference） method，是MC和DP 方法的一个结合。相比MC方法，TD除了能够适用于连续任务外，和MC的差异从下图可以清楚看到。MC需要回退整个序列更新Q值，而TD只需要回退1步或n步更新Q值。因为MC需要等待序列结束才能训练，而TD没有这个限制，因此TD收敛速度明显比MC快，目前的主要算法都是基于TD。下图是TD和MC的回退图，很显然MC回退的更深。