DQN (Nature)

一、 算法流程:
定义可配置参数
初始化
- 初始化 replay buffer 大小N
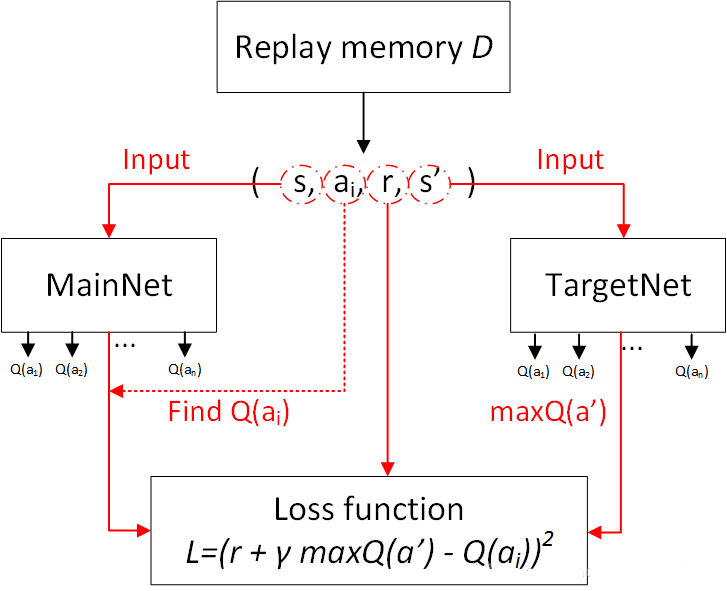
- 初始化 Q 网络 $Q$ ,使用随机权值 $\theta$
- 初始化 TargetQ 网络 $\hat{Q}$ 权值 $\theta^-$,使用 Q 网络的权值 $\theta$
DQN 一个Episode的流程
- 使用 $\epsilon-greedy$ 策略 选择一个 action $a_t$
- 执行当前 action $a_t$, 获取下一个状态 $s_{t+1}$ 和 reward $r_{t}$
- 将当前状态$s_t$赋值为下一个状态 $s_{t+1}$
- 将五元组$\langle s_t,a_t,r_t,s_{t+1},done \rangle $存入 replay buffer $D$
- 训练Q网络$Q$:
- [Pre-condition]训练网络的前提是 replay buffer 的已有五元组数量大于 batch size $N$
- 从 replay buffer $D$中随机选取 batch size $N$条数据$\langle s_j,a_j,r_j,s_{j+1},done\rangle$ $D_{selected}$
- 计算目标Q值$y$, $y$是一个向量,$\{y_j \in y |j\in[0,N]\} $,大小为 batch size $N$
- 当 $D_{selected}$[j] 中 $done=True$ 时,即终局状态,此时 $y_j=r_j$
- 当 $D_{selected}$[j] 中 $done=False$ 时,即非终局状态,此时$y_i=r_j+\gamma max_{a’}\hat{Q}(s_{j+1},a’;\theta^-)$, 注意这里是用的 TargetQ 网络进行的
- 使用优化器进行梯度下降,损失函数是(一个batch里面) $(y-Q(s,a;\theta))^2$,注意这里使用的是Q网络进行,来让计算出来的目标Q值与当前Q网络输出的Q值进行MSE
- 每 $C$ 次 episode,soft update 一次 target net 参数,$\theta^- = \theta$
不断迭代Episode流程$M$次
二、对应代码
完整代码地址: Nature DQN
初始化
- 初始化 replay buffer 大小N
- 初始化 Q 网络 $Q$ ,使用随机权值$\theta$
- 初始化 TargetQ 网络 $\hat{Q}$ 权值 $\theta^-$,使用 Q 网络的权值 $\theta$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
def create_Q_network(self):
"""
Q net 网络定义
:return:
"""
# 输入状态 placeholder
self.state_input = tf.placeholder("float", [None, self.state_dim])
# Q 网络结构 两层全连接
with tf.variable_scope('current_net'):
W1 = self.weight_variable([self.state_dim, 100])
b1 = self.bias_variable([100])
W2 = self.weight_variable([100, self.action_dim])
b2 = self.bias_variable([self.action_dim])
h_layer = tf.nn.relu(tf.matmul(self.state_input, W1) + b1)
# Q Value
self.Q_value = tf.matmul(h_layer, W2) + b2
# Target Net 结构与 Q相同,可以用tf的reuse实现
with tf.variable_scope('target_net'):
W1t = self.weight_variable([self.state_dim, 100])
b1t = self.bias_variable([100])
W2t = self.weight_variable([100, self.action_dim])
b2t = self.bias_variable([self.action_dim])
h_layer_t = tf.nn.relu(tf.matmul(self.state_input, W1t) + b1t)
# target Q Value
self.target_Q_value = tf.matmul(h_layer_t, W2t) + b2t
t_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='target_net')
e_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='current_net')
# soft update 更新 target net
with tf.variable_scope('soft_replacement'):
self.target_replace_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
#===============================================================#
def weight_variable(self, shape):
"""
初始化网络权值(随机, truncated_normal)
:param shape:
:return:
"""
initial = tf.truncated_normal(shape)
return tf.Variable(initial)
#===============================================================#
def bias_variable(self, shape):
"""
初始化bias(const)
:param shape:
:return:
"""
initial = tf.constant(0.01, shape=shape)
return tf.Variable(initial)
$\epsilon-greedy$ 策略 定义,这里对$\epsilon$进行一个随时间步的迁移而减小的策略,使其动作选择的不确定性逐渐减小。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def egreedy_action(self, state):
"""
epsilon-greedy策略
:param state:
:return:
"""
Q_value = self.Q_value.eval(feed_dict={
self.state_input: [state]
})[0]
if random.random() <= self.epsilon:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return random.randint(0, self.action_dim - 1)
else:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return np.argmax(Q_value)
Replay buffer的定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26def perceive(self, state, action, reward, next_state, done):
"""
Replay buffer
:param state:
:param action:
:param reward:
:param next_state:
:param done:
:return:
"""
# 对action 进行one-hot存储,方便网络进行处理
# [0,0,0,0,1,0,0,0,0] action=5
one_hot_action = np.zeros(self.action_dim)
one_hot_action[action] = 1
# 存入replay_buffer
# self.replay_buffer = deque()
self.replay_buffer.append((state, one_hot_action, reward, next_state, done))
# 溢出出队
if len(self.replay_buffer) > REPLAY_SIZE:
self.replay_buffer.popleft()
# 可进行训练条件
if len(self.replay_buffer) > BATCH_SIZE:
self.train_Q_network()
Q网络训练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28def train_Q_network(self):
"""
Q网络训练
:return:
"""
self.time_step += 1
# 从 replay buffer D中随机选取 batch size N条数据<s_j,a_j,r_j,s_j+1,done> D_selected
minibatch = random.sample(self.replay_buffer, BATCH_SIZE)
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
next_state_batch = [data[3] for data in minibatch]
# 计算目标Q值y
y_batch = []
Q_value_batch = self.target_Q_value.eval(feed_dict={self.state_input: next_state_batch})
for i in range(0, BATCH_SIZE):
done = minibatch[i][4]
if done:
y_batch.append(reward_batch[i])
else:
y_batch.append(reward_batch[i] + GAMMA * np.max(Q_value_batch[i]))
self.optimizer.run(feed_dict={
self.y_input: y_batch,
self.action_input: action_batch,
self.state_input: state_batch
})
Soft update
1
2
3def update_target_q_network(self, episode):
# 更新 target Q netowrk
if episode % REPLACE_TARGET_FREQ == 0:
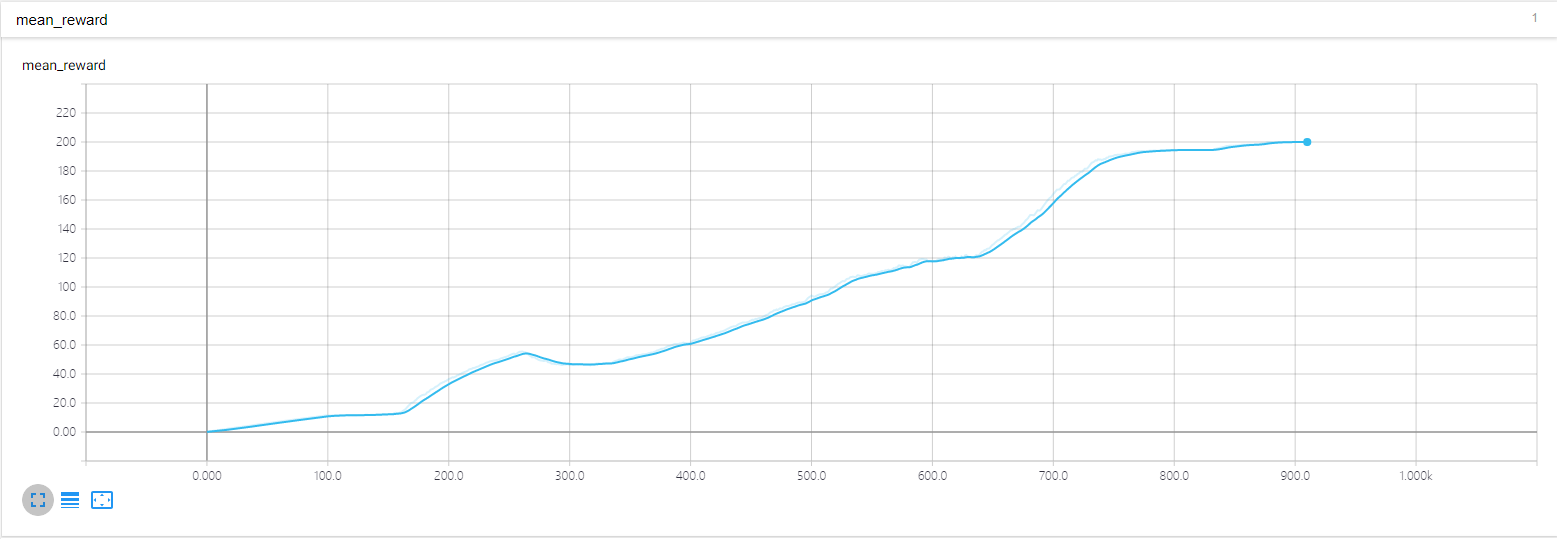
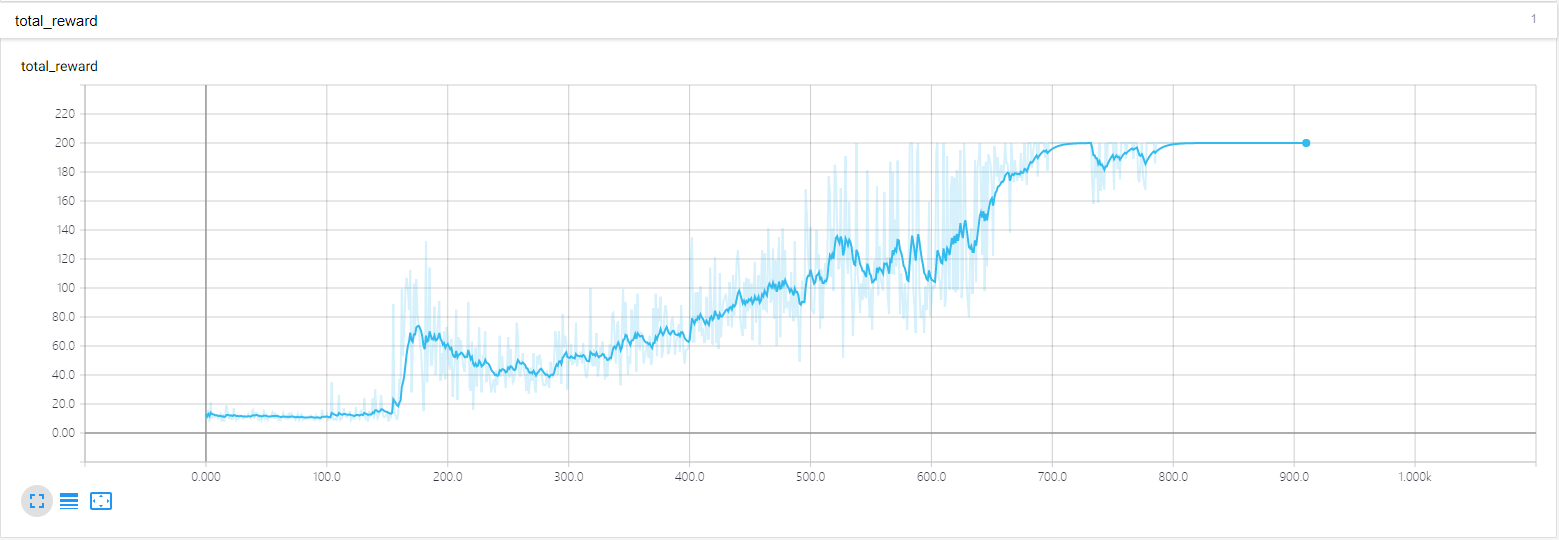
三、实验结果
环境 cart-pole-v0 (期望回报是200)
四、DQN参考论文流程:

五、Double DQN
DQN存在的问题是Q function容易过拟合,根据状态 $s_{t+1}$ 选择动作 $a_{t+1}$ 的过程,以及估计 $Q(s_{t+1},a_{t+1})$ 使用的同一个Q net网络参数,这可能导致选择过高的估计值,从而导致过于乐观的值估计。为了避免这种情况的出现,可以对选择和衡量进行解耦,从而就有了使用 Double DQN 来解决这一问题。
Double DQN与DQN的区别仅在于$y$的求解方式不同,Double DQN根据Q网络参数来选择动作$a_{t+1}$,再用Target Q网络参数来衡量$Q(s_{t+1},a_{t+1})$的值。
反映在代码上,就是训练的时候选择Q的时候有点变动:
1 | def train_Q_network(self): |
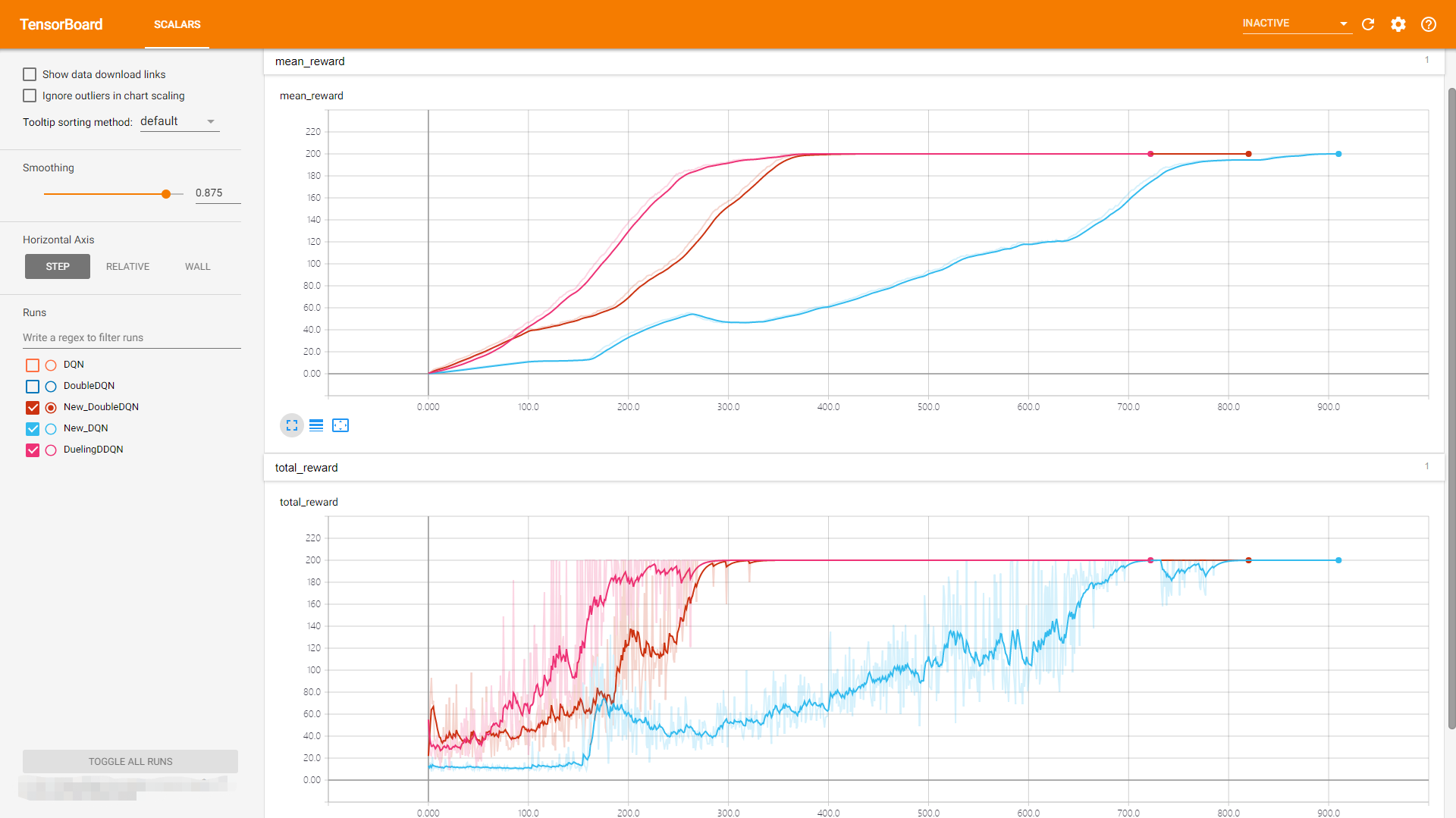
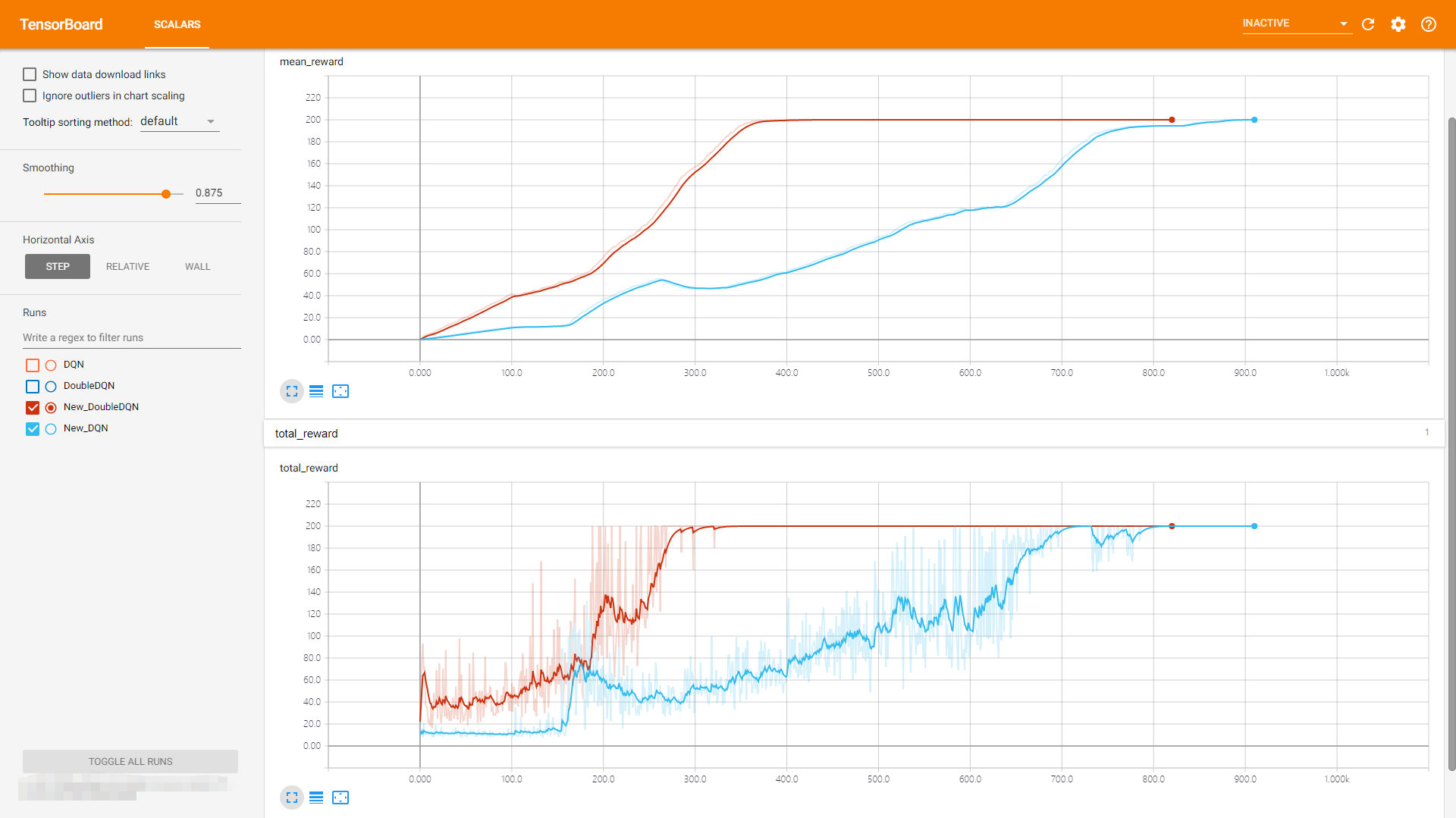
六、DQN,DDQN实验结果对比
可以看到DoubleDQN的表现比 DQN稳定
七、 Dueling DDQN
八、 Dueling DQN, DDQN, DQN对比