深度学习优化器

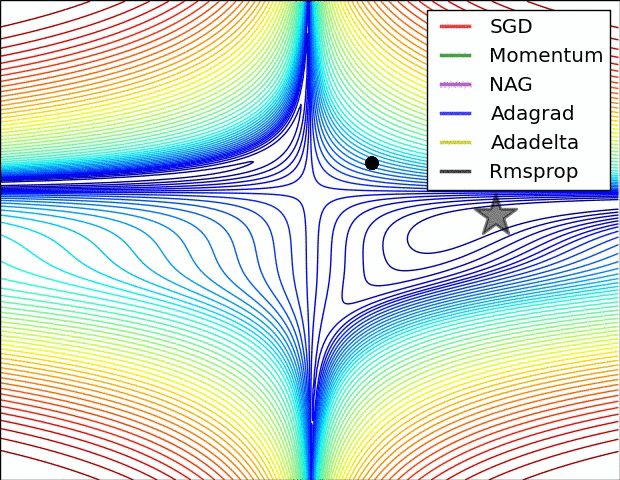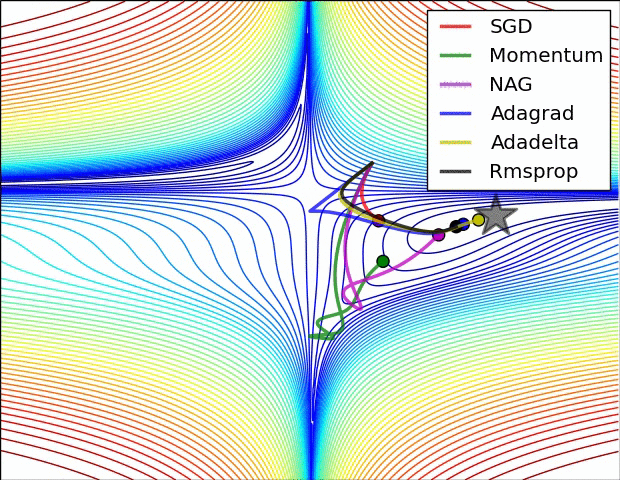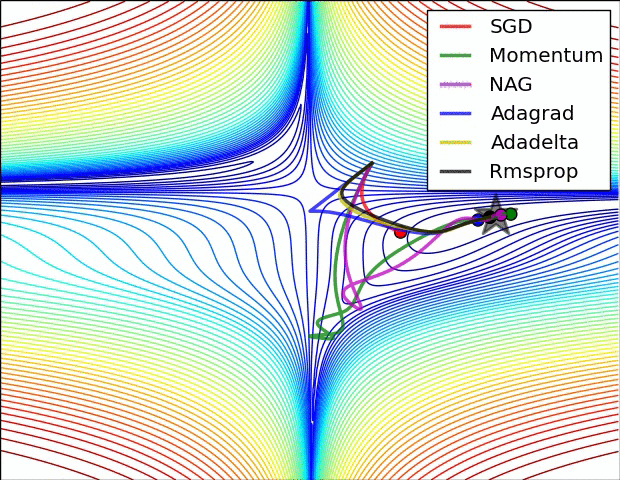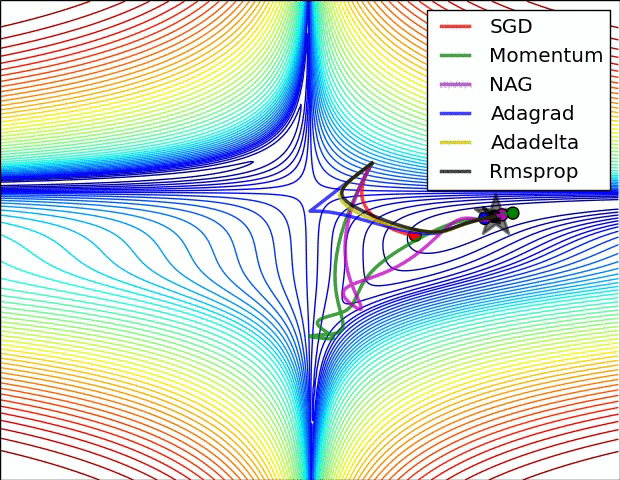
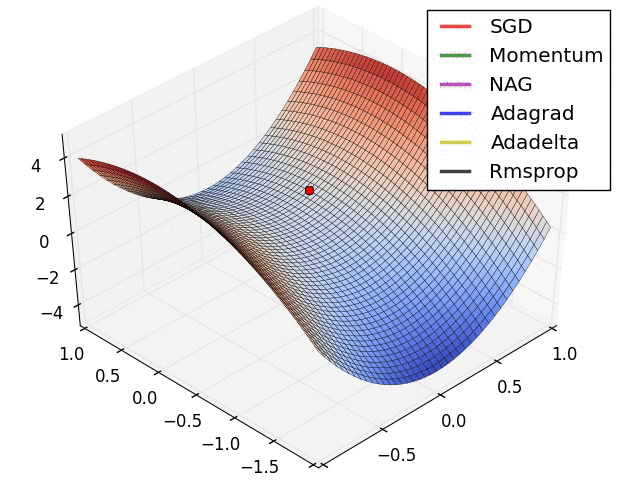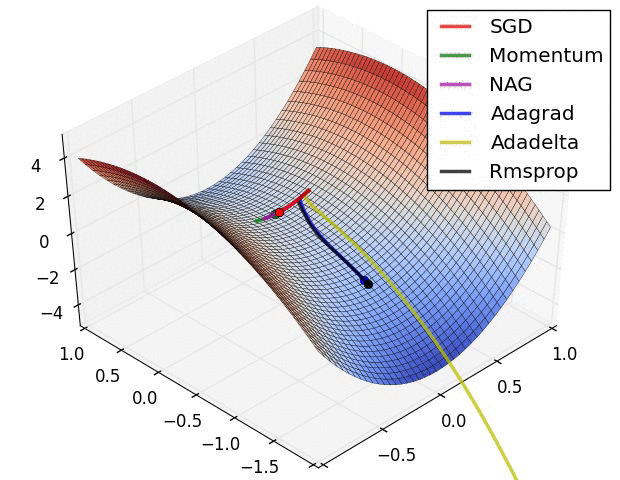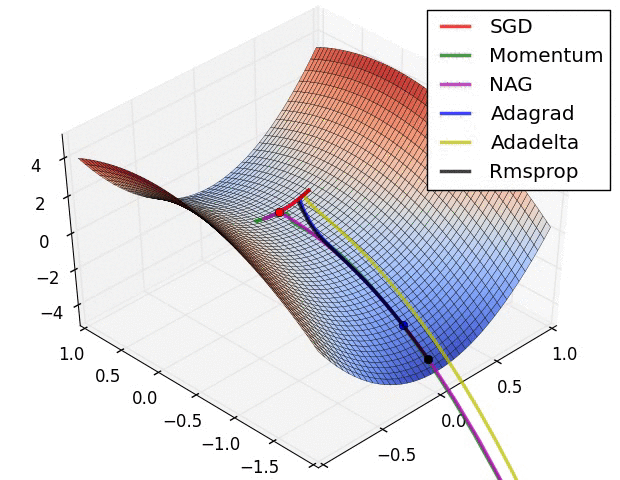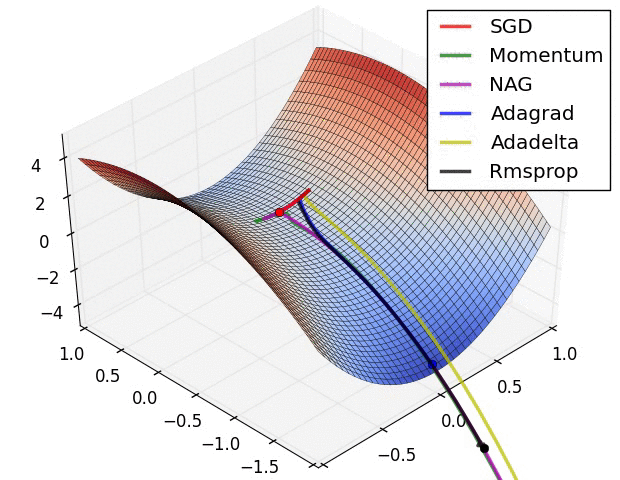
参考资料：深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

1. 随机梯度下降

批梯度下降(Gradient Descent)
随机批梯度下降(Stotastic Gradient Descent)
- 每次梯度计算只使用一个随机样本(可能是噪声样本)
  - 避免在类似的样本上进行冗余计算
  - 增加了跳出当前局部最小值的可能
  - 可以通过减小学习率，来使其能够与GD有相同的收敛速度
小批量随机梯度下降(Mini batch SGD)
- 每次梯度计算使用小批量的样本
  - 梯度计算比单样本计算更加稳定
  - 便于使用矩阵计算
  - 适当的batch size训练效率高

def gradient_decent(_x_data, _y_data, _b, _w, _iteration, _lr):
    """
    Gradient Decent
    :param _x_data:
    :param _y_data:
    :param _b:
    :param _w:
    :param _iteration:
    :param _lr:
    :return:
    """
    _b_history = [_b]
    _w_history = [_w]

    for _i in range(_iteration):
        b_grad = 0.0
        w_grad = 0.0

        for _n in range(len(x_data)):
            b_grad = b_grad - 2.0 * (y_data[_n] - _b - _w * _x_data[_n]) * 1.0
            w_grad = w_grad - 2.0 * (y_data[_n] - _b - _w * _x_data[_n]) * _x_data[_n]

        _b = _b - _lr * b_grad
        _w = _w - _lr * w_grad

        _b_history.append(_b)
        _w_history.append(_w)
    return _b_history, _w_history

2. 随机梯度下降的困难

局部梯度的反方向不一定是函数整体的下降方向。
学习率衰减法，难以根据数据进行自适应。
对不同的参数采取不同的学习率(数据稀疏，不平衡)。
容易困在局部最小点，甚至是鞍点。

3. 动量方法(Momentum)

目的: 解决随机梯度的局部梯度的反方向不一定是函数整体的下降方向问题。
方法：
- 动量法：(Momentum)（适用于隧道型曲面）
  - 方法：
    
    每次更新都吸收上一次更新的余势。使得主体方向得到了更好的保留，使得效果被不断的放大。
    $v_t = \gamma v_{t-1}+\eta\nabla_{\theta}J(\theta) \\ \theta_t=\theta_{t-1}-v_t$
  - 缺点：
    
    在前期下降比较快，收敛速度较好，但到最优值附近时容易由于动量过大而导致优化过度。
- 改进动量法：(Nesterov)
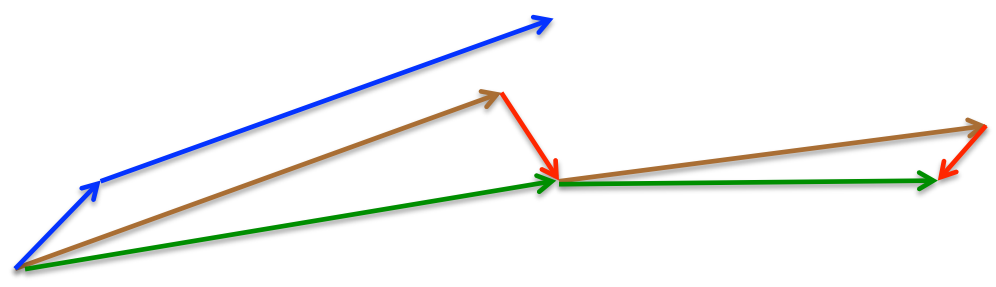
  - 方法：利用主体的下降方向，预判下一步优化的位置，根据预判的位置计算优化的梯度。 $v_t = \gamma v_{t-1} + \eta \nabla_{\theta}J(\theta-\gamma v_{t-1}) \\ \theta=\theta-v_t$ momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)

4. 自适应梯度方法(Ada)

目的：
- 解决学习率衰减法，难以根据数据进行自适应的问题。
- 更新频繁的参数使用较小的学习率。
- 更新较少的参数使用较大的学习率。
方法：
- Adagrad方法：
  - 思路：Adagrad对每个参数的历史梯度更新进行叠加，并以此作为下一次更新的惩罚系数。（约束学习率）
  - 算法：
    - 梯度：$g_{t,i}=\nabla_{\theta}J(\theta_i)$
    - 梯度历史矩阵: $G_t$是对角阵，其中$G_{t,ii}=\sum_{k}g_{k,i}^2$
    - 参数更新：（历史梯度大，则$\eta$项越小）
  - 存在的问题：
    - 1. 随着训练的进行，学习率衰减过快。
    - 1. 梯度与参数单位不匹配

def adagrad(_x_data, _y_data, _b, _w, _iteration, _lr):
    """
    Adagrad: auto adapt the learning rate.
    root mean square
    :param _x_data:
    :param _y_data:
    :param _b:
    :param _w:
    :param _iteration:
    :param _lr:
    :return:
    """
    _b_history = [_b]
    _w_history = [_w]
    lr_b = 0
    lr_w = 0
    epsilon = 0.01
    for _i in range(_iteration):
        b_grad = 0.0
        w_grad = 0.0

        for _n in range(len(x_data)):
            b_grad = b_grad - 2.0 * (y_data[_n] - _b - _w * _x_data[_n]) * 1.0
            w_grad = w_grad - 2.0 * (y_data[_n] - _b - _w * _x_data[_n]) * _x_data[_n]

        lr_b = lr_b + b_grad ** 2
        lr_w = lr_w + w_grad ** 2
        _b = _b - _lr / (np.sqrt(lr_b) + epsilon) * b_grad
        _w = _w - _lr / (np.sqrt(lr_w) + epsilon) * w_grad

        _b_history.append(_b)
        _w_history.append(_w)
    return _b_history, _w_history

RMSprop（Adadelta方法第一版）：
- 目的：解决随着训练的进行，学习率衰减过快。
- 思路：使用梯度平方的移动平均来取代全部的历史平方和。
- 算法：
  - 梯度：$g_{t,i}=\nabla_{\theta}J(\theta_i)$
  - 移动平均: $\mathbb{E}_{t}[g^2]=\gamma \mathbb{E}_{t-1}[g^2] + (1-\gamma) g_{t}^2$
  - 参数更新：（更新系数分母换了）
    $\theta_{t+1, i} = \theta_{t,i} - \frac{\eta}{\sqrt{\mathbb{E}_{t,ii}+\epsilon}} \cdot g_{t,i}$
- 特点：
  - 其实RMSprop依然依赖于全局学习率
  - RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间
  - 适合处理非平稳目标
  - 对于RNN效果很好

Adadelta方法第二版:
- 目的：梯度与参数单位不匹配
- 思路：使用参数更新的移动平均来取代学习率$\eta$
- 算法：
  - 参数更新: （学习率换成参数的移动平均自适应） $\theta_{t+1, i} = \theta_{t,i} - \frac{\sqrt{\mathbb{E}_{t-1}[\Delta \theta]}}{\sqrt{\mathbb{E}_{t,ii}+\epsilon}} \cdot g_{t,i}$
- 特点：
  - 训练初中期，加速效果不错，很快
  - 训练后期，反复在局部最小值附近抖动

5. 动量+自适应方法(Adam)

Adam （带动量项的RMSprop）
- 思路：在Adadelta的梯度平方和(二阶矩)的基础上引入动量方法的的一阶矩(梯度)
- 算法：
  - 一阶矩(动量)： $m_t=\beta_1 m_{t-1}+(1-\beta_1)g_t$ （保持下降速度）
  - 二阶矩(Adadelta)：$v_t=\beta_2 v_{t-1}+(1-\beta_2)g_t^2$ （保持参数自适应）
  - 参数更新：
- 特点：
  - 经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。
  - 适用于大数据集和高维空间
NAdam (引入Nesterov)
- 对学习率有了更强的约束